Written by daweibayu
on July 22, 2017

Poj 1737「男人八题」

题目

男人八题之 Connected Graph 题目内容可以看上边链接，这里不在赘述。就是求 n 个不同点的无向连通图有多少种可能。

解题思路

我们假设，当点为 n 个时： a(n) 为无向连通图的个数。 b(n) 为无向不连通图的个数。 c(n) 为总个数。很显然，c(n) = a(n) + b(n); 其中 c(n) = $2^{(n(n-2)/2)}$ ，b(n) = $\sum_{i=1}^{n-1}C(n,i-1)a(i)*c(n-i)$ 简书貌似不支持数学符号，那就是:

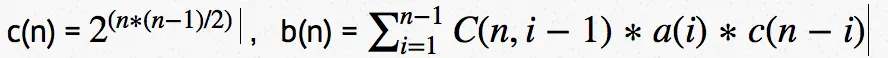
证明

上边给出的 c(n) 与 b(n) 的公式大家可能比较懵逼，我们来证明一下。

c(n)

先求出 n 个不同点可以有多少种连线，就是 C(n,2)，C(n,2) = n*(n-1)/2，如果对这个有疑问的话，可以去看一下高数中排列组合部分。
对于没组连线，都有两种状态，一种是相连，一种是不相连，一共有 C(n,2) 组连线，所以总共的种类为 2^C(n,2)，即

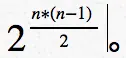
b(n)

c(n) 是已知的，如果想求 a(n)，只要求出 b(n) 就可以了。我们在 n 个点中随意取一个点 A，A 的状态一共有以下几种：

1. A 与所有其他点都不连通。
2. A 只与其他点中的一个点连通。
3. A 只与其他点中的两个点连通。
……
i. A 只与其他点中的 i - 1 个点联通。
……
n-1. A 只与其他点中的 n-2 个点连通。

这就是所有的情况，那我们只要把每种状态都计算出来然后相加，就是 b(n) 了，那接下来我们计算一下：

1. C(n,0)*a(1)*c(n-1)
2. C(n,1)*a(2)*c(n-2)
3. C(n,2)*a(3)*c(n-3)
……
i. C(n,i-1)*a(i)*c(n-i)
……
n-1. C(n,n-2)*a(n-1)*c(1)

代码

import java.math.BigInteger;
import java.util.Scanner;
import java.io.*;

public class Main {
	static BigInteger[] unConnected = new BigInteger[51];
	static BigInteger[] connected = new BigInteger[51];
	static BigInteger[] total = new BigInteger[51];

	// 为了方便，factorial[i] 为 i 的阶乘
	static BigInteger[] factorial = new BigInteger[51];

	/**
	 * 初始化阶乘（避免重复运算）
	 */
	private static void initFactorial() {
		factorial[0] = BigInteger.valueOf(1);
		factorial[1] = BigInteger.valueOf(1);
		for (int i = 2; i <= 50; i++) {
			factorial[i] = factorial[i - 1].multiply(BigInteger.valueOf(i));
		}
	}

	/**
	 * 获取排列组合结果
	 */
	private static BigInteger getCombination(int total, int select) {
		if (select == 0) {
			return BigInteger.valueOf(1);
		}
		return factorial[total].divide(factorial[select].multiply(factorial[total - select]));
	}

	/**
	 * 获得不连通图的数量，比如 10 个点的不连通图数量， 这里 num 应该为 10（而不是 9）
	 */
	private static BigInteger getNnConnected(int num) {
		BigInteger sum = BigInteger.valueOf(0);
		for (int i = 1; i <= num - 1; i++) {
			sum = sum.add(getCombination(num - 1, i - 1).multiply(connected[i]).multiply(total[num - i]));
		}
		return sum;
	}

	public static void main(String[] args) {

		// 初始化阶乘表
		initFactorial();

		unConnected[0] = BigInteger.valueOf(0);
		connected[0] = BigInteger.valueOf(0);
		total[0] = BigInteger.valueOf(0);

		// 计算总数、非连通图数、连通图数
		for (int i = 1; i <= 50; i++) {
			total[i] = BigInteger.valueOf(2).pow(i * (i - 1) / 2);
			unConnected[i] = getNnConnected(i);
			connected[i] = total[i].subtract(unConnected[i]);
		}

		// 输入与输出
		Scanner sc = new Scanner(System.in);
		while (sc.hasNext()) {
			int n = sc.nextInt();
			if (n == 0) {
				return;
			}
			System.out.println(connected[n]);
		}
	}
}

你没看错，我怂了，实在不想用 C++ 再写一遍大数运算，我用了 java……

← → Top